import matplotlib.pyplot as plt
def plot_vector_addition(v1, v2):
plt.figure(figsize=(10, 8)) # Increased figure size
# Draw first vector
plt.quiver(0, 0, v1[0], v1[1], angles='xy', scale_units='xy', scale=1, color='r', label='v1')
# Draw second vector (from origin)
plt.quiver(0, 0, v2[0], v2[1], angles='xy', scale_units='xy', scale=1, color='b', label='v2')
# Draw sum vector
plt.quiver(0, 0, v1[0]+v2[0], v1[1]+v2[1], angles='xy', scale_units='xy', scale=1, color='g', label='v1+v2')
# Draw second vector (from end of first vector)
plt.quiver(v1[0], v1[1], v2[0], v2[1], angles='xy', scale_units='xy', scale=1, color='b', linestyle='--')
plt.grid(True)
plt.axis('equal')
# Set axis limits with padding
max_val = max(abs(v1).max(), abs(v2).max(), abs(v1+v2).max())
plt.xlim(-max_val-1, max_val+1)
plt.ylim(-max_val-1, max_val+1)
plt.legend()
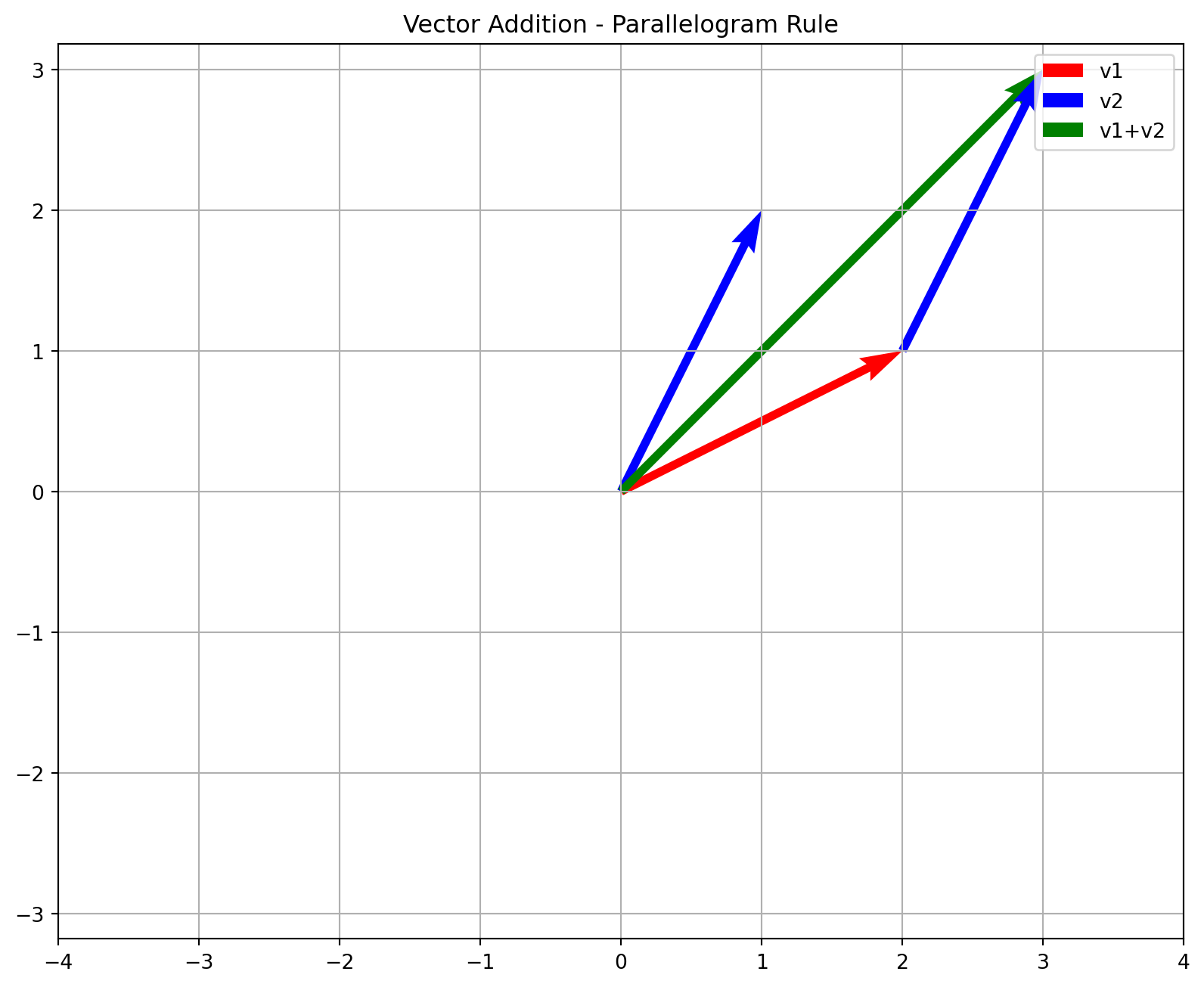
plt.title('Vector Addition - Parallelogram Rule')
plt.show()
# Demonstrate 2D vector addition
v1_2d = np.array([2, 1])
v2_2d = np.array([1, 2])
plot_vector_addition(v1_2d, v2_2d)