什么是位图?
位图(Bitmap)是计算机中存储图像的一种基本格式。在这种格式中,图像被分割成一个个小方格(像素),每个方格用二进制数字来存储颜色信息。
计算机如何存储位图?
- 存储结构
- 计算机使用二进制(0和1)存储所有数据
- 位图将图像分解成规则的网格,每个网格点就是一个像素
- 每个像素占用固定的存储空间(比特数)
- 常见的位图格式
- BMP:最基本的位图格式
- PNG:支持无损压缩的位图格式
- JPEG:支持有损压缩的图片格式
- 不同类型图片的存储方式
import numpy as np
import matplotlib.pyplot as plt
# 1. 黑白图片(1位/像素)
bw_image = np.zeros((10, 10)) # 只用0和1表示
bw_image[2:8, 2:8] = 1
# 2. 灰度图片(8位/像素)
gray_image = np.zeros((10, 10))
gray_image[2:8, 2:8] = 128 # 0-255之间的值
# 3. 彩色图片(24位/像素 = 3×8位)
color_image = np.zeros((10, 10, 3)) # 3个通道:红、绿、蓝
color_image[2:8, 2:8, 0] = 1 # 红色通道
# 创建一个包含3个子图的图表
plt.figure(figsize=(15, 5))
# 显示黑白图像
plt.subplot(1, 3, 1)
plt.imshow(bw_image, cmap='binary')
plt.title('Black and White Image')
plt.axis('off') # 关闭坐标轴
# 显示灰度图像
plt.subplot(1, 3, 2)
plt.imshow(gray_image, cmap='gray')
plt.title('Grayscale Image')
plt.axis('off')
# 显示彩色图像
plt.subplot(1, 3, 3)
plt.imshow(color_image)
plt.title('Color Image (Red)')
plt.axis('off')
# 调整子图之间的间距
plt.tight_layout()
# 显示图表
plt.show()
手写数字图像示例
让我们通过实际的手写数字图像来理解位图:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
# 加载手写数字数据集
digits = load_digits()
X = digits.images # 图像数据
y = digits.target # 标签(实际的数字)
# 选择第一个数字作为示例
sample = X[0]
# 展示图像及其矩阵值
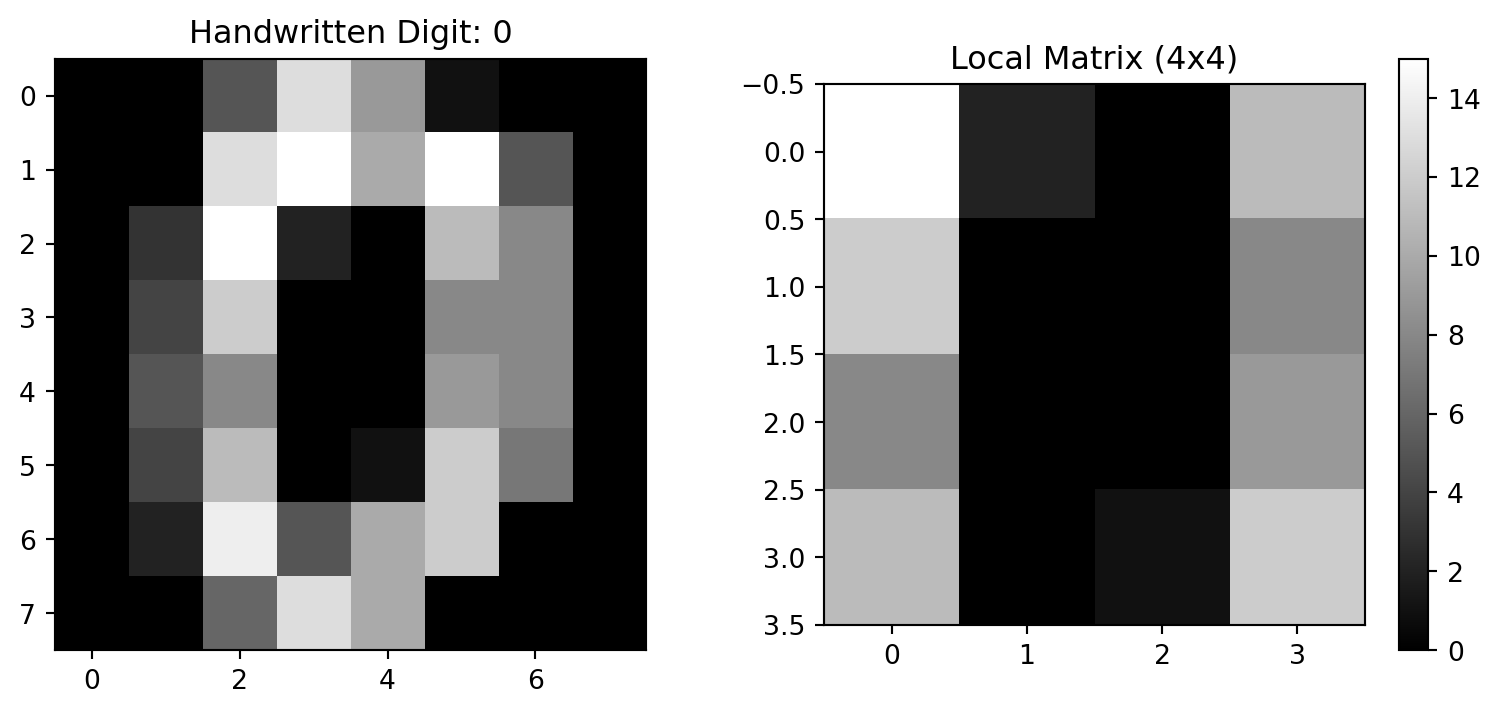
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.imshow(sample, cmap='gray')
plt.title(f'Handwritten Digit: {y[0]}')
plt.subplot(122)
plt.imshow(sample[2:6, 2:6], cmap='gray')
plt.title('Local Matrix (4x4)')
plt.colorbar()
plt.show()
print("图像局部(4x4区域)的实际矩阵值:")
print(sample[2:6, 2:6])
图像局部(4x4区域)的实际矩阵值:
[[15. 2. 0. 11.]
[12. 0. 0. 8.]
[ 8. 0. 0. 9.]
[11. 0. 1. 12.]]
理解图像矩阵
在这个数据集中: - 每个图像是 8×8 像素的矩阵 - 每个像素值范围是 0-16: - 0 表示最暗(黑色) - 16 表示最亮(白色) - 中间值表示不同程度的灰色
基本图像处理示例
让我们看看一些简单的矩阵运算如何改变图像:
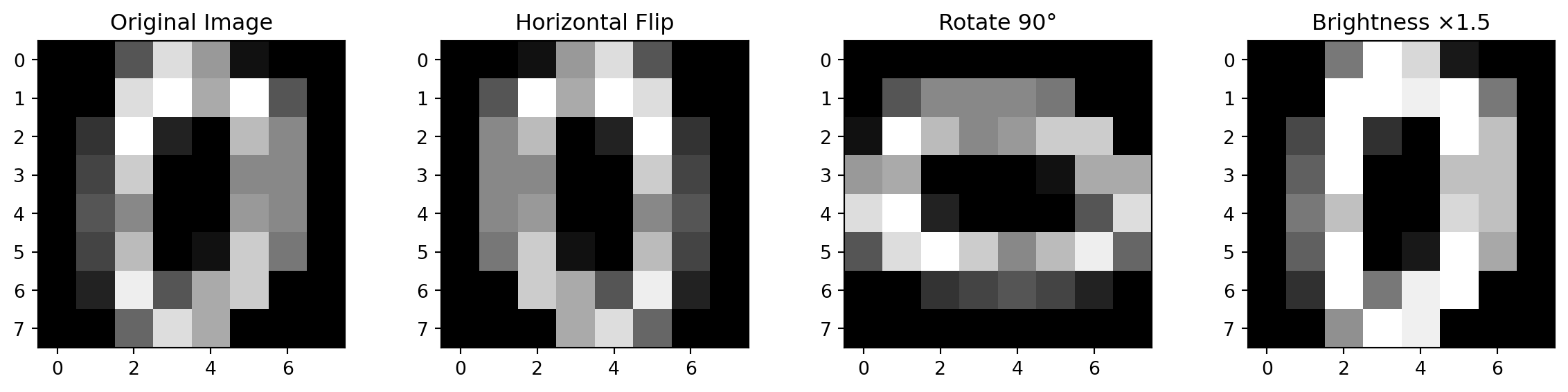
plt.figure(figsize=(15, 3))
# 原始图像
plt.subplot(141)
plt.imshow(sample, cmap='gray')
plt.title('Original Image')
# 水平翻转
plt.subplot(142)
flipped = np.fliplr(sample) # 矩阵左右翻转
plt.imshow(flipped, cmap='gray')
plt.title('Horizontal Flip')
# 旋转90度
plt.subplot(143)
rotated = np.rot90(sample) # 矩阵旋转
plt.imshow(rotated, cmap='gray')
plt.title('Rotate 90°')
# 增加亮度
plt.subplot(144)
brighter = np.clip(sample * 1.5, 0, 16) # 所有值乘以1.5
plt.imshow(brighter, cmap='gray')
plt.title('Brightness ×1.5')
plt.show()
print("让我们看看这些操作如何改变矩阵的值:")
local_area = sample[2:6, 2:6]
print("\n原始区域的矩阵值:")
print(local_area)
print("\n增加亮度后的矩阵值(×1.5):")
print(np.clip(local_area * 1.5, 0, 16))
让我们看看这些操作如何改变矩阵的值:
原始区域的矩阵值:
[[15. 2. 0. 11.]
[12. 0. 0. 8.]
[ 8. 0. 0. 9.]
[11. 0. 1. 12.]]
增加亮度后的矩阵值(×1.5):
[[16. 3. 0. 16. ]
[16. 0. 0. 12. ]
[12. 0. 0. 13.5]
[16. 0. 1.5 16. ]]
多个数字示例
让我们看看不同的手写数字是如何存储的:
# 显示前5个数字
plt.figure(figsize=(15, 3))
for i in range(5):
plt.subplot(1, 5, i+1)
plt.imshow(X[i], cmap='gray')
plt.title(f'Digit: {y[i]}')
plt.axis('off')
plt.show()
小结
- 图像在计算机中是以数字矩阵的形式存储的
- 每个像素对应矩阵中的一个数字:
- 图像处理实际上就是对矩阵进行数学运算:
- 翻转矩阵 = 翻转图像
- 旋转矩阵 = 旋转图像
- 矩阵数值变化 = 图像亮度变化
- 这种表示方法让计算机能够: